試聴映像
- 1. 具体的な速度設定で検証できるデニソフ氏の式
- 2. デニソフ氏による長さの変換式の導出
- 3. デニソフ氏の最大の失敗とは
映像を観る
概要
前回は負の領域におけるデニソフ変換の式を導出した。今回は負の領域において、長さの変換式が成り立つかどうかの検証を行う。また、デニソフ変換を利用して長さの変換式を導出してみる。
映像編集者のオススメポイント
-
デニソフ氏の主張がなぜ納得できないのか? の説明は、デニソフ氏自身も「そうだったのか~!」と、何処かで納得しているのではないかと思います。(^^)
-
デニソフ変換を幾何学的に理解する秘訣は、、、“自分で絵を描いてみて、いくつかやってみる”ことだそうです! なかなか実践しようとしない自分の背中を、誰かに押してほしい。。。次回からは速度の合成則です。いっちょまえに予告だけしときます。
目次
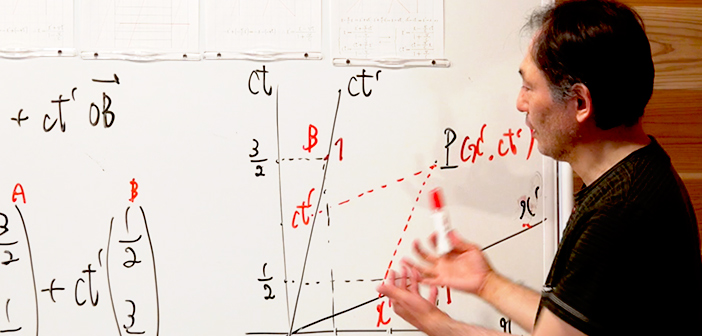
1.速度を v=c/3 とした場合の斜交座標 (00:00:00)
具体的な例として、速度を v=c/3 とした場合に、どのようなミンコフスキー図が描かれるかを示してみる。
2.速度を v=c/3 とした場合の葉巻型UFOの位置と長さ (00:09:04)
同様にv=c/3の時に、ガリレイ変換的座標平面とミンコフスキー図の両方で、静止座標系から葉巻型UFOの位置がどのように見えるのかを具体的に示し、デニソフ氏の式との一致を検証してみる。加えて、なぜミンコフスキー図の負領域で、ctとct'、xとx'が傾き1のラインで一致するのかを検証する。
3.静止座標系から見た葉巻型UFOの長さの式の導出 (00:35:07)
これまでは具体例で説明してきた。今度は無駄なものを一切省いた抽象的な図を用いて、デニソフ氏の提示する、静止座標系から見た葉巻型UFOの長さの式 l(エル)1 = l(エル)/(1−v/c) を導出してみる。
4.通り過ぎるロケットから見た葉巻型UFOの長さの式の導出 (00:53:10)
次は同様に、通り過ぎるロケットから見える静止した葉巻型UFOの長さの式 l(エル)2 = l(エル)/(1+v/c) を導出してみる。
5.デニソフ氏の最大の失敗と次回の講義 (01:15:43)
デニソフ氏の最大の失敗は、負の領域の式を示さなかったことであり、これが物理学者らに彼の理論が受け入れられなかった要因と思われる。今回でその不備を補ったので、次回からはデニソフ変換における速度の合成則を取り上げる。
終わり(01:20:45)
※詳しい目次は、映像を購入してログインすると見ることができます。










3件のコメント
正の領域と負の領域で変換式が違うのが盲点でしたね。同じなら話は簡単だったのに。
デニソフの相対性理論の前提は変数が正の領域に限定されていた。しかし、負の領域まで拡張できたことを理解しました。次は光速を超える物体の動きがどう見えるか?デニソフ理論に基づいた式と図でどう描かれるのか?を知りたいですね。
負の領域を式で示したことで、これでようやくデニソフ変換の不備を補ったとのこと。記念すべきデニソフ変換の完成!ともいえるわけですね。これから、アインシュタインの相対性理論で一番大事だとおもわれる速度の合成則とデニソフ変換が一致を見ていくとのこと。光速を超える領域のお話、何とも楽しみです!