【お知らせ】
本日27日(日)より、日曜日の時事ブログの記事は基本的に3本となります。————————————————————————

第3回 純正律
純正律と周波数の比率
純正律の音の決め方
前回、純正律とは、「倍音という法則をもとに、音を重ねたときに調和するような」音律だと説明しました。
具体的には、ドレミファソラシドの各音の周波数が、次の比率になるように音を決めていきます。
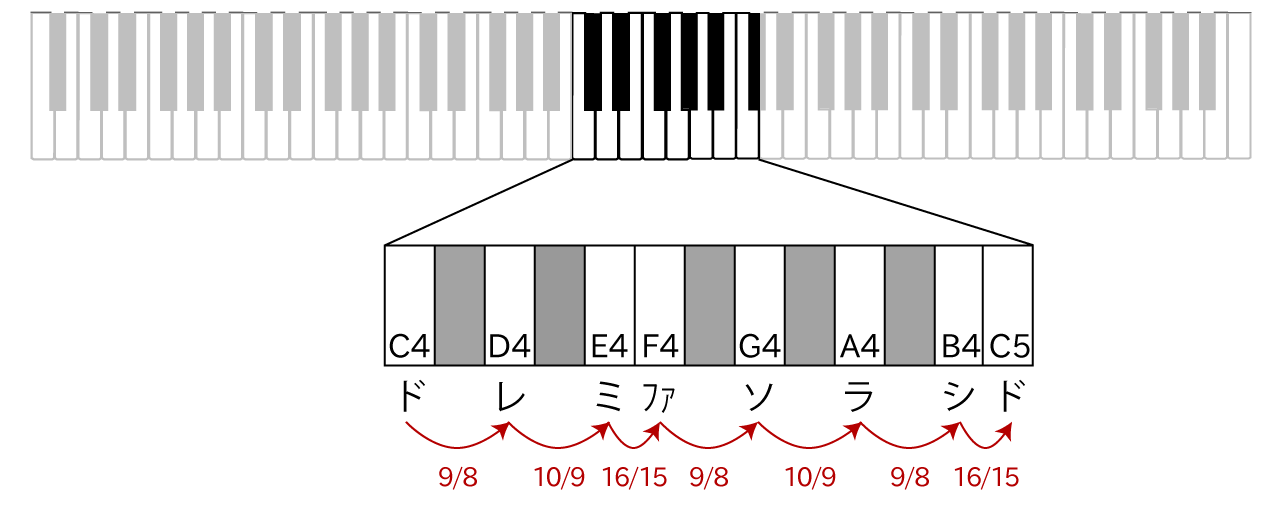
- ドに対してレの周波数は9/8
- レに対してミの周波数は10/9
- ミに対してファの周波数は16/15
- ファに対してソの周波数は9/8
- ソに対してラの周波数は10/9
- ラに対してシの周波数は9/8
- シに対してドの周波数は16/15
すべて単純な整数比ですね。例えば、ラをA4=440Hzとしたときの、“ハ長調音階の”各音の周波数を出してみると、次のようにきれいな整数になります。
- ド(C4)の周波数は 264Hz
- レ(D4)の周波数は 297Hz
- ミ(E4)の周波数は 330Hz
- ファ(F4)の周波数は 352Hz
- ソ(G4)の周波数は 396Hz
- ラ(A4)の周波数は 440Hz
- シ(B4)の周波数は 495Hz
- ド(C5)の周波数は 528Hz
純正律と平均律の和音の聴き比べ
上の純正律の周波数を用いた音と、平均律の周波数を用いた音とで、和音のサンプルを作りました。ひとまずここで、その2つを聴いていただきます。
①純正律:
②平均律:
①の純正律の方が、うなりのなさとともに、世界の広さを感じるような気がしませんか? ここはひとつ、心の目で両足を見る方法でリラックスして聴き比べてみてください。
和音の周波数比の違い
上のサンプルは、それぞれ次の和音を順に鳴らしています。
a. ド-ミ-ソ (長三和音)
b. ファ-ラ-ド (長三和音)
c. ソ-シ-レ (長三和音)
d. ミ-ソ-シ (短三和音)
e. ラ-ド-ミ (短三和音)
①の純正律の場合、それぞれの和音の周波数の比率を出してみると、次のようになります。
a. 264 : 330 : 396 = 4 : 5 : 6
b. 352 : 440 : 528 = 4 : 5 : 6
c. 396 : 495 : 297×2 = 4 : 5 : 6
d. 330 : 396 : 495 = 10 : 12 : 15
e. 440 : 528 : 330×2 = 10 : 12 : 15
きれいな小さい整数比ですね。つまり倍音の関係にある音同士なので、美しい和音の響きが得られるということになります。
②の平均律の方はどうでしょうか。平均律の周波数値を当てはめてみましょう:
a. 261.63 : 329.63 : 392.00
b. 349.23 : 440.00 : 523.26
c. 392.00 : 493.88 : 587.32
d. 329.63 : 392.00 : 493.88
e. 440.00 : 523.26 : 659.26
これはどうやったって小さな整数比として考えるのは無理で、あくまで倍音という視点は全く考慮されていない音律ということになります。
純正律の欠点 〜 なぜ平均律が普及したのか?
純正律で美しい和音が出ない場合
純正律の方が明らかに美しい音楽が作れそうなものですが、純正律にも欠点があります。次の和音を考えてみます。
f. レ-ファ-ラ (短三和音)
g. シ-レ-ファ (減三和音)
それぞれの周波数の比率を出してみると、次のようになります。
f. 297 : 352 : 440 = 27 : 32 : 40
g. 495 : 594 : 704 = 45 : 54 : 64
ここまで数字が大きくなると、倍音の関係からは外れるようです。つまり純正律が倍音を意識した音律といっても、どんな和音の組み合わせも美しいというわけにはいかないようです。
となると、ある問題が出てきます。さきほど純正律の各音の周波数を出す所で、「“ハ長調音階の”」とわざわざ付けたところに注目してください。次のように、“ハ長調音階の”純正律で調律した鍵盤で、二短調の曲を演奏をすると考えてみます。
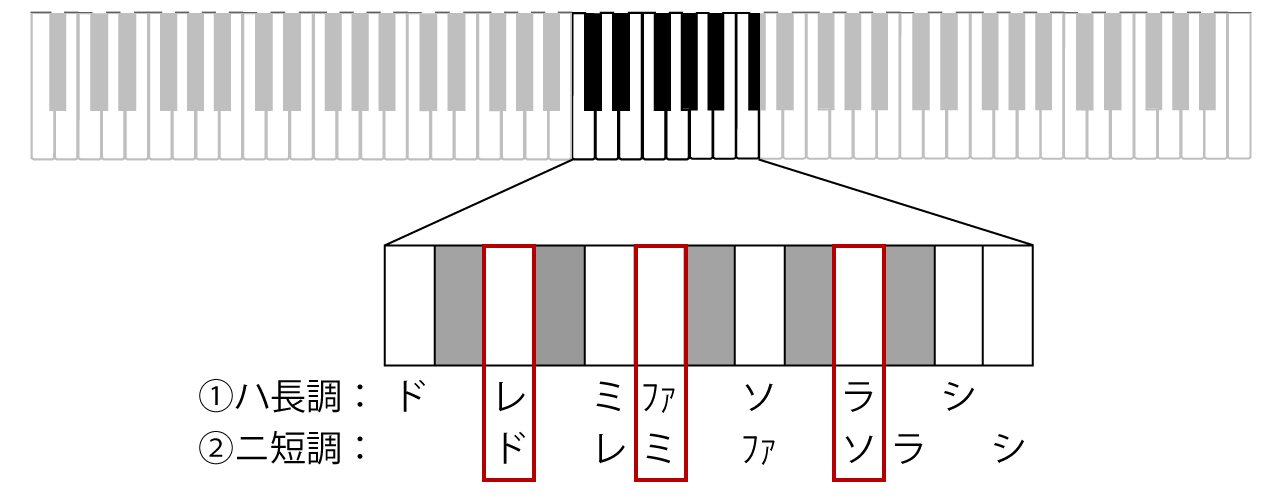
①がハ長調音階、②が二短調音階です。これで、②のド-ミ-ソ(長三和音)を鳴らすと、この鍵盤は、“ハ長調音階の”純正律で調律しているので、上の「f. レ-ファ-ラ(短三和音)」を鳴らしていることと同じです。これは美しくない和音の組み合わせになってしまいます。
純正律の欠点
ニ短調の曲を演奏するには、あくまでニの音をド(主音)として調律する必要があります。これだと、次の点で困ります。
- 曲の調性が途中で変わる「転調」に対応できない。(転調のたびに、それに合わせて調律した楽器に取り替えないといけない。)
- 調性の異なる楽器同士の合奏が難しい。
上で挙げたものはあくまで欠点の1つです。他にも、合唱で用いると段々音がずれていく問題など、様々な問題があります。
このような純正律の欠点を改良するために、中全音律をはじめ、色々な改良版(不等分平均律、あるいは不等分音律という)が考えられました。しかし、最終的には、純正律とはまったく別の考え方に基づく「平均律」(十二等分平均律ともいう)の方が普及したということのようです。
次回は、やっと調和純正律の話です。
◇ コラム:小さな整数比の和音がなぜ美しい? ◇
上記で、「数字が大きくなると、倍音の関係からは外れるようです」と書きました。
倍音の定義というのは、基音の整数倍の周波数の音でした。それであれば、上の和音f. の周波数297 : 352 : 440 は、11×27 : 11×32 : 11×40となり、この和音は11Hzの倍音同士の組み合わせではないのかという疑念が出てきます。
しかし、その理屈でいくと、平均律の和音a.の周波数261.63 : 329.63 : 392.00だって、その比率を26162:32963:39000とすれば、1Hzの倍音同士ではないかという話になってしまいます。ですので、「整数倍なら倍音」といっても、その数字にはどうやら限度があるようです。
そこで、与えられた3つの音の周波数の組み合わせについて、次の2つを調べるプログラムを作ってみました。
- ハモりの数 … 音成分同士の周波数の一致(ただし±1Hzの差は許容)
- うなりの数 … 音成分同士で生じる"うなり"のうち、人間が認識できそうな0.5〜20回/秒の間にあるものの数。
この記事に出てきた周波数の組み合わせについて、プログラムを実行した結果は以下の表のとおりです。なお、倍音成分の数は第5倍音成分までを考慮しています。(倍音とうなりとハモりの関係については前回のコラムを参照してください。)
| No. | 周波数と比率 | ハモりの数 | うなりの数 |
|---|---|---|---|
| 純正律の和音(小さい整数比の例) | |||
| 1 | 264 : 330 : 396 (4 : 5 : 6) | 2 |
0 |
| 2 | 352 : 440 : 528 (4 : 5 : 6) | 2 |
0 |
| 3 | 396 : 495 : 594 (4 : 5 : 6) | 2 |
0 |
| 4 | 330 : 396 : 495 (10 : 12 : 15) | 2 |
0 |
| 5 | 440 : 528 : 660 (10 : 12 : 15) | 2 |
0 |
| 純正律の和音(大きな整数比の例) | |||
| 6 | 297 : 352 : 440 (27 : 32 : 40) | 1 |
1 |
| 7 | 495 : 594 : 704 (45 : 54 : 64) | 0 |
0 |
| 平均律の和音 | |||
| 8 | 261.63 : 329.63 : 392.0 | 1 |
2 |
| 9 | 349.23 : 440.0 : 523.26 | 0 |
2 |
| 10 | 392.0 : 493.88 : 587.32 | 0 |
2 |
| 11 | 329.63 : 392.0 : 493.88 | 0 |
2 |
| 12 | 440.0 : 523.26 : 659.26 | 0 |
1 |
こうしてみると、次のことがわかります。
- 小さい整数比の和音(No.1〜5)は、倍音成分同士がハモり、またうなりがないので、美しい。
- 大きい整数比の和音(No.6〜7)になると、ハモりの数が減るか、あるいはうなりがあらわれる。よって、和音の響きが物足りないか、あるいは濁りを感じられる。
- 平均律のような複雑な比の和音(No.8〜12)は、ハモりがほとんどなく、うなりが必ず生じる。よって、濁りを感じられる。
つまり、小さい整数比の周波数同士の組み合わせの和音ほど、美しい和音が出やすくなるといえます。
今回はプログラムで検証してみましたが、他にもリサージュ図形というものを用いて視覚的に比較する方法もあるようです。

Author:アレッシオ・ダマート[CC BY-SA]
リサージュ図形
この記事は、シャンティ・フーラによる執筆記事です。音楽の分野に詳しい方におかれましては、もし間違いや説明上改善すべき点などがありましたら、ご指摘やご意見をいただければ幸甚です。ぜひ、こちらのコメント欄にフィードバックをお寄せください。





時事ブログは2012年に始まって以来、1日5本のペースをほぼ欠かすことなく発信を続けてきました。これはひとえに竹下氏の、世界が平和になるまで休むわけにはいかないとの強い思いと、それに呼応する編集部・ライターの皆様の尽力によるものでした。
しかし、無理をしていては続かないということで、このたびブログ開設以来の空前の働き方改革を行うことになりました。なお、日によって重要な情報がある場合などは、記事が3本よりも増えることもあります。
今後とも時事ブログをご愛読賜りますよう、よろしくお願いいたします。
さて、前回は、各音名の音の高さを決める要素である、周波数と音律について説明しました。また、現在広く使われている平均律の仕組みと、過去に使われていた「純正律」と呼ばれる音律に触れました。その純正律を理解する上で必要な、「倍音」という仕組みも紹介しました。
今回は、その純正律を倍音の知識をもとに本格的に説明します。なぜ現在広く使われている平均律に満足しない人が多いのか、今回の記事でその理由がよくわかると思います。
なお、本稿にあたっては、西洋音楽史家・坂崎紀氏の「音律入門」を大いに参考にし、特に純正律における和音の例と周波数比はこちらの文献の数字を基にいたしました。貴重な資料を公開してくださっていることに謝意を表します。