————————————————————————

第2回 周波数と音律
音の高さと周波数
音は波である
音の高さは周波数によって決まります。周波数について説明するために、まず音がどのように表現されるのかを説明します。
どのような音も、波として表現されます。次の映像をご覧ください。
ピアノを弾き、その音をマイクを通してコンピュータに録音させると、波状のデータが記録されます。これを再生すると、同じ音がスピーカーから再生されます。皆さんが使っているCDも、同じ原理です。音をスタジオで録音したものを、CDに波状のデータとして書き込んで持ち運び、これを家庭のプレイヤーで再生すると同じ音が出るというわけです。
波の間隔で変わる音の高さ
さて、このピアノの各音は、同じ音色ですが、音の高さが違います。その違いは、波の間隔にあります。ミ・ソ・ドの、3つの音の波の形を比較してみましょう:
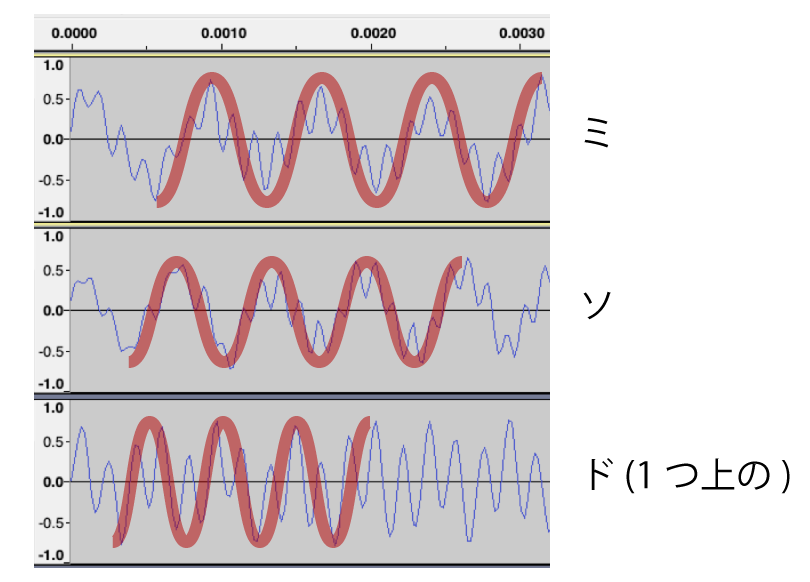
細かいギザギザが混じっているので、それを取り除いた一番大きな波を、赤い線で示しています。この赤い線を見ると、高い音ほど、波の間隔が狭いことにお気づきでしょうか。この波の間隔の狭さをあらわす数字を、周波数といいます。
周波数
周波数を説明する上で、より単純な波の音をコンピュータで作り出してみます。次の映像をご覧ください。
前回の記事で、音名 A4(ハ長調のラ)の音の高さは 440Hz という周波数に決まっていると書きました。映像では、この440Hzの周波数を持つものすごくシンプルな音(正弦波、あるいはサイン波という)を作り出し、その波を見ています。
その波の最初の部分を拡大したのが次の画像です:
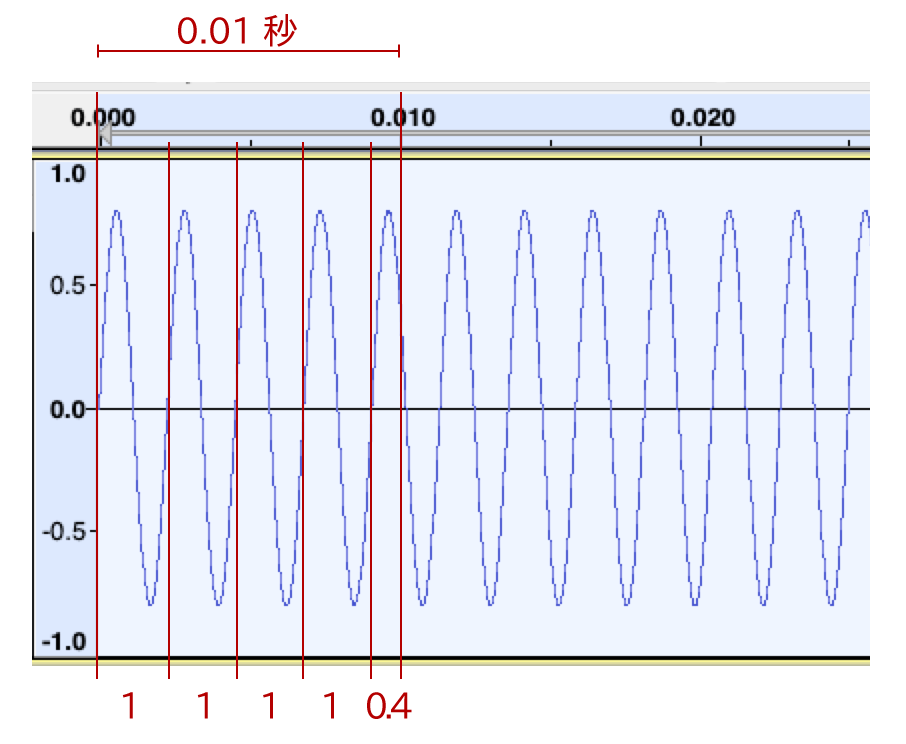
波が上がって下がってまた上がるまでを1回とすると、 0.01 秒で 1 + 1 + 1 + 1 + 0.4 = 4.4 回、上がり下がりしています。つまり1秒間で、 4.4 ÷ 0.01 = 440 回上がり下がりします。この440という数字に Hz (ヘルツ)を付けたものが周波数です。
この上がり下がりが速い(周波数が高い)ほど、波の間隔が狭く、音が高くなります。逆に遅い(周波数が低い)ほど、波の間隔が広く、音が低くなります。実際に、この波の周波数を変えた3つの音を聴いてみましょう。
次を再生すると、音の低い方から順に ③半分の220Hz → ①440Hz → ③倍の880Hz が鳴ります:
さて、再生してみると、3つの音同士は何だか相性がいいように感じませんか? 実は、低い方から、1オクターヴ下のラ(A3 = 220Hz) → ラ(A4 = 440Hz) → 1オクターヴ上のラ(A5 = 880Hz) の周波数です。
実は同じラの仲間でした。つまり、オクターヴというのは、実は、周波数を2倍するごとに、1つ上がっていくようになっています。
(音が波であることや周波数について、もっと詳しく知りたい方は、広島大学大学院理学研究科 小林亮教授による「音の波と三角関数」の資料をご覧ください。わかりやすい説明で面白いです。)
音律と平均律
音律とは、あるひとつの音を基準音として、そこからドレミファソラシドの音の周波数をどのように決めるかというルールです。
現代で広く使われている音律は「平均律」といいます。非常に単純な次の式で、どんな音名の周波数も出すことができます。

nに、 A4 = 440Hz から半音いくつ分ズレた位置の音なのかの数字を入れればいいのです。これだけで、国際的な各音の周波数の出来上がりです。
試しに、第4オクターヴのハ長調のドレミファソラシドの音の周波数を出すと次の通りです:
| 階名と音名 | n (A4からの半音差) | 周波数の計算式 |
|---|---|---|
| ド(C4) | n = -9 | 440 × (12√2)^-9 = 261.63 Hz |
| レ(D4) | n = -7 | 440 × (12√2)^-7 = 293.66 Hz |
| ミ(E4) | n = -5 | 440 × (12√2)^-5 = 329.63 Hz |
| ファ(F4) | n = -4 | 440 × (12√2)^-4 = 349.23 Hz |
| ソ(G4) | n = -2 | 440 × (12√2)^-2 = 392 Hz |
| ラ(A4) | n = 0 | 440 × (12√2)^0 = 440 Hz |
| シ(B4) | n = 2 | 440 × (12√2)^2 = 493.88 Hz |
| ド(C5) | n = 3 | 440 × (12√2)^3 = 523.25 Hz |
一つの数字(国際標準なら440Hz)と一つの式で全部の音の高さが決まってしまいます。数学的にはシンプルで美しいですね。しかし、この音の高さの決め方に満足しない人がたくさんいます。そこで、純正律というものに触れることになります。
純正律とは?
純正律は過去に広く使われていた音律です。純正律は、どのようにして音の高さを決めるのでしょうか? ここで、倍音という仕組みを説明します。
倍音と純正律
倍音とは、ある音を基準にしたときに(「基音」という)、その音の周波数の、整数倍の周波数の音のことです。次の音を聴いてみてください。
①
4つの音が、ハモっていますね。では次を聴いてみてください。
②
似てはいますが、②は後の音が多い方になるほどに、うるさく、聴き続けていられない感じを受けないでしょうか。
①の音は、220Hz、440Hz、660Hz、880Hzの4つの音の重ね合わせです。続いての②の音は、220Hz、435Hz、665Hz、875Hzの4つの音の重ね合わせです。
①の音は、220Hz に x1、x2、x3、x4 と整数を掛けた周波数になっています。このように、倍音の関係の音同士を重ねると、響きが調和します。いっぽう、②の音は、それにわずか ±5Hz を加えることで倍音の関係から外しました。このように倍音の関係から外れた音は、重ね合わせた時に不快な響き(うなり)が生まれます。
昔の人はこの倍音という法則をもとに、音を重ねたときに調和するようなドレミファソラシドの音の高さを考えました。こうして、音の自然な法則から必然的に生まれたのが「純正律」という音律です。
次回は純正律の紹介と、なぜそれが使われなくなってしまったのかを説明したいと思います。
◇ コラム:倍音とうなりとハモり ◇
倍音とうなり、ハモりの関係について、このコラムでより詳しく説明しておきます。上で聴いていただいた倍音のサンプルですが、重ね合わせた音のひとつであるラ(A4 = 440Hz)の音の波は次のようになっています。
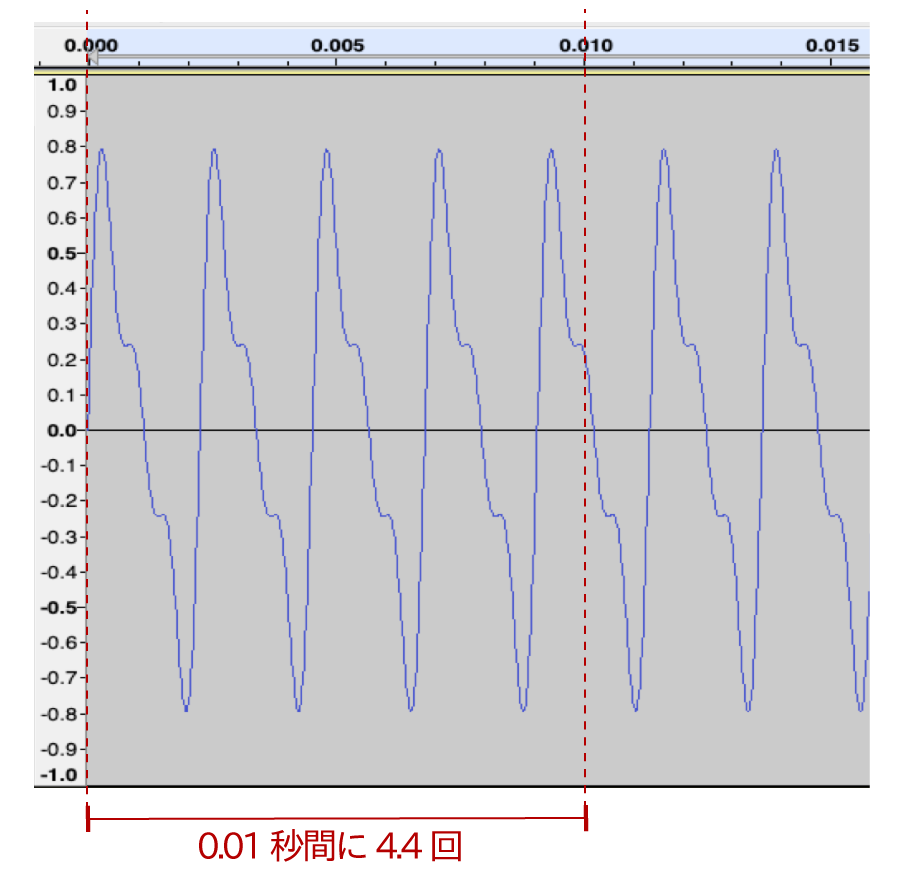
前述の、コンピュータで作り出したシンプルな440Hzの音の波と同じく、0.01秒間に4.4回波が上がり下がりしています。しかし、それにしてはやけにギザギザしています。これは、実は440Hz以外の周波数の波が混ざっているのです。
ここで「周波数解析」という方法を使うと、他にどんな周波数の波が、どれくらい混ざっているのかを調べられます。周波数解析の結果を見てみましょう:
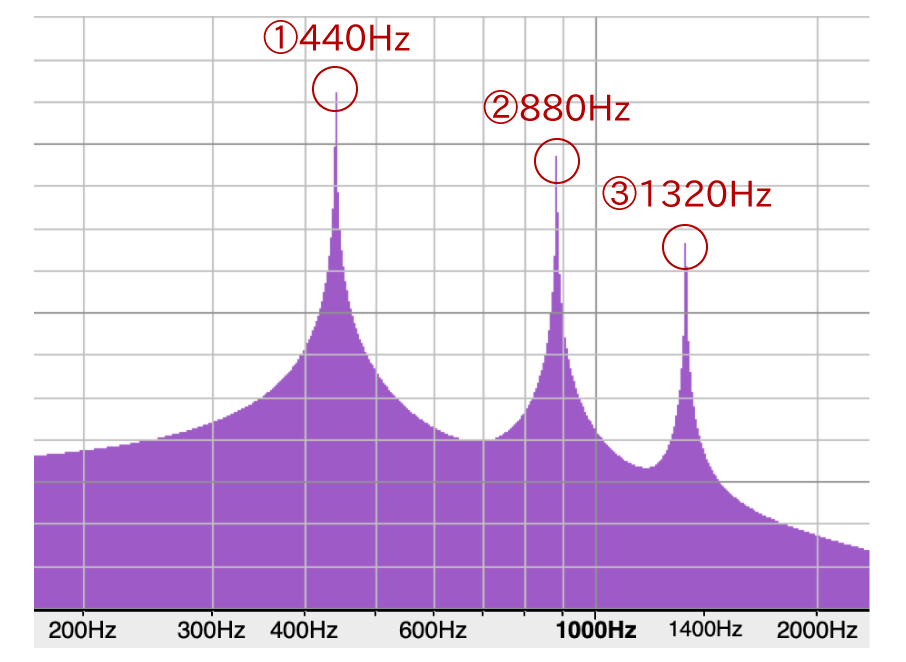
この図で、山が飛び出ている箇所が、その周波数の音が含まれていることを示しています。また、山の高さが高いほど、その周波数の音が大きく含まれています。このサンプルの音では、一番高い①440Hzの山、次に高い②880Hzの山、最後に一番低い③1320Hzの山があります。
この①②③は、②は440Hz×2 = 880Hz、③は440Hz×3=1320Hzと、②・③は①の倍音であることにお気づきでしょうか。このように、ある音の中に混じっている②・③の音のことを、それぞれ「第2倍音成分」「第3倍音成分」といいます。①は「基音成分」といいます。
実は、楽器が出す高低のある音のことを「楽音」といいますが、そのような音は、すべてこのような倍音成分がいくつも入っています。上で「不快な響き(うなり)が生まれます」と書きましたが、実はこのうなりに大きく関係しているのは、②と③の倍音成分です。
次はサンプルで用いた音と、それに含まれる音成分の周波数を、表にしたものです。
| サンプルで用いた音 | ①基音成分 | ②第2倍音成分 | ③第3倍音成分 | |
|---|---|---|---|---|
| a. | 440Hz (220Hz×2倍) |
440Hz | 880Hz | 1320Hz |
| b. | 660Hz (220Hz×3倍) |
660Hz | 1320Hz | 1980Hz |
| c. | 665Hz (220Hz×3倍から+5Hzずらした音) |
665Hz | 1330Hz | 1995Hz |
倍音の関係にあるa.とb.の音がハモるのは、①②③の各成分のいずれの音の周波数も、それぞれ遠く離れているか、あるいは一致するかのどちらかであるためです。
しかし、倍音の関係から外れているa.とc.の音は、a.の③の1320Hzとc.の②の1330Hzに、10Hzの差があります。a.とc.の音を重ねたとき、この倍音成分同士の間にできるわずかな差は、うなり(不快な響き)を生み出します。
さらに、倍音の関係にない875Hzの音d.を加えると、今度は、a.の②とd.の①に5Hzの差が生まれ、これもうなりを生み出します:
| サンプルで用いた音 | ①基音成分 | ②第2倍音成分 | ③第3倍音成分 | |
|---|---|---|---|---|
| a. | 440Hz (220Hz×2倍) |
440Hz | 880Hz | 1320Hz |
| d. | 875Hz (220Hz×4倍から-5Hzずらした音) |
875Hz | 1750Hz | 2625Hz |
これが、倍音の関係から外れた音同士にうなりが生じる理由です。うなりは、その音の周波数(基音の周波数)だけで起こるものではなく、さらにその音の倍音成分が影響して起こるものだということです。
さて、このように生じるうなりの有る無しが、重ねた音の快・不快に影響するということがわかりました。この「うなり」とは別に、例えば、a.の③の1320Hzとb.の②の1320Hzが一致するというふうに、倍音成分の周波数が一致することも、重ねた音がハモると感じられる要因のようです。
私はこうした、うなりの少なさと倍音の一致の多さが、純正律を理解する上での音の協和の主要な要素だと一応理解しています。しかし、他にも周期の一致を脳が気持ちよく感じるからという見解もあります。倍音と和音の関係は、中々奥が深いようです。
この記事は、シャンティ・フーラによる執筆記事です。音楽の分野に詳しい方におかれましては、もし間違いや説明上改善すべき点などがありましたら、ご指摘やご意見をいただければ幸甚です。ぜひ、こちらのコメント欄にフィードバックをお寄せください。





前回は、音楽で用いられる「ドレミファソラシド」は階名といい、オクターヴや調性(キー)によって、音の高さが変わってしまうこと。また、音の高さをはっきりさせた音の名前を音名といい、「C4」などと表現されることを説明しました。今回は、ある音名の音の高さを決める要素である、周波数と音律について説明します。