————————————————————————

第12回 【発展編】周波数の解析
離散フーリエ変換
音声データの周波数を解析するには、離散フーリエ変換という手法を用います。
音声が波として表現できることは、第2回で説明しました。この波は、周波数成分の和で表現することができます。
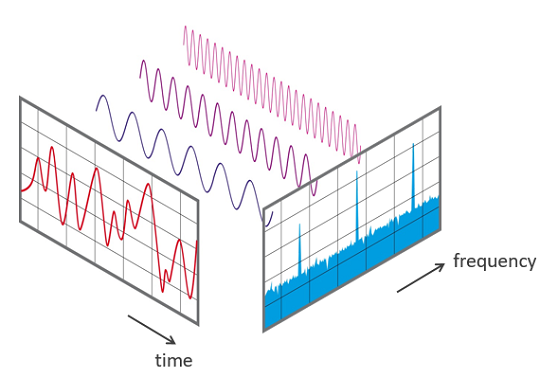
離散フーリエ変換の概念
出典:Author:Phonical [CC-BY SA]
左の方に、音声データの波が赤で描かれています。その後ろ側に、周波数の異なるいくつもの紫色の単純な波があります。これは、赤い音声データの波は、幾つもの紫色の単純な波の合成で表現できることを示しています。
紫色の波は単純なサイン波です。この紫色の波ひとつは、周波数(Frequency)と、その波の強さ(波の上がり下がりの大きさで、これを振幅(Amplitude)という)で表すことができます。
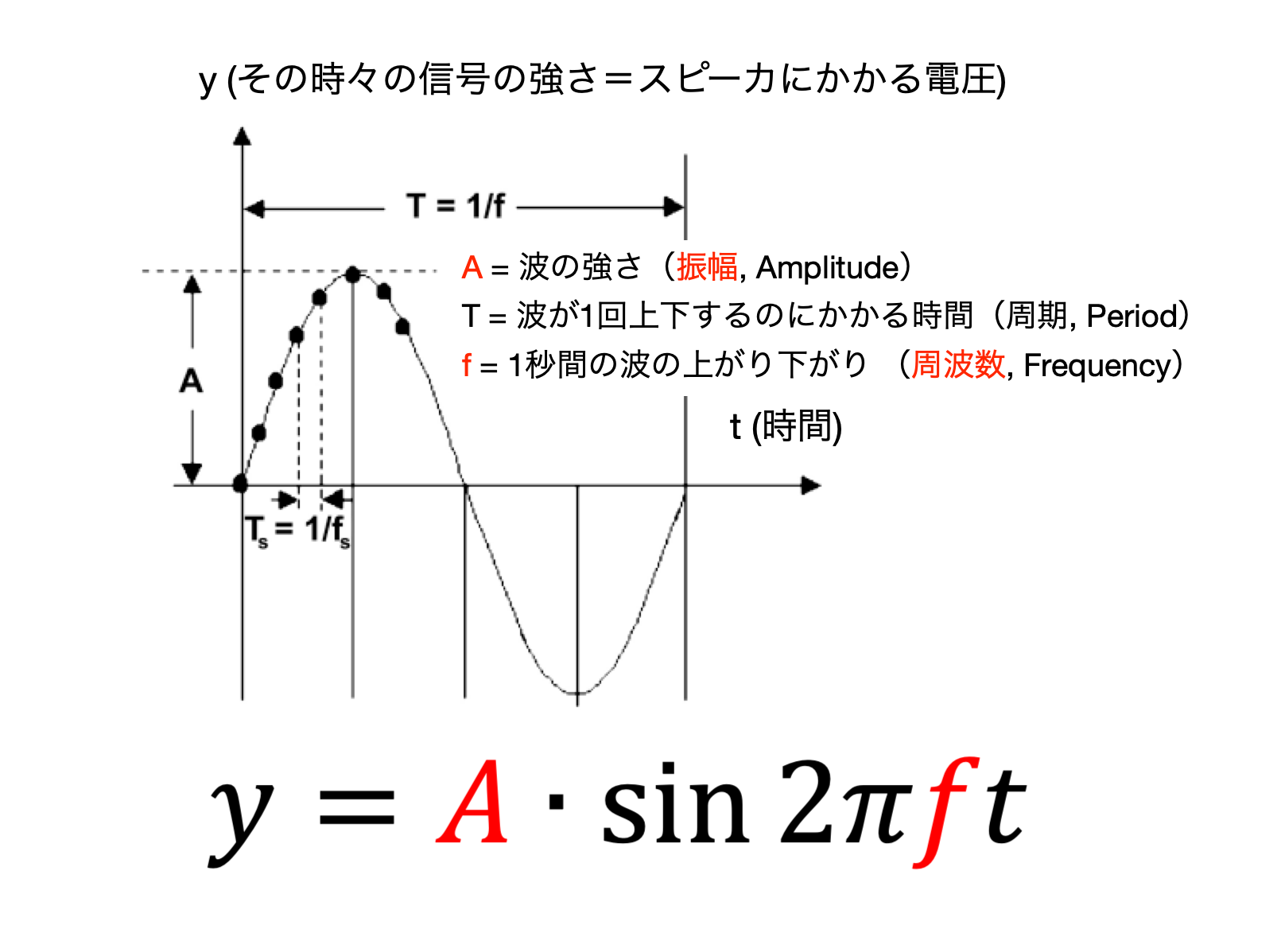
単純なサイン波は、振幅(A)と周波数(f)だけで表現できる
(図はこちらを元に筆者作成)
ですので、このA(振幅)をグラフの縦軸、f(周波数)をグラフの横軸とすれば、幾つもの紫色の波を1つのグラフで表現できます。このグラフが、先の「離散フーリエ変換の概念」の図の、右の青色のグラフです。これが離散フーリエ変換による周波数解析の結果となります。
要するに、離散フーリエ変換とは、次の1.から3.までを一飛に行う計算です。
- 赤色の波(パソコンやCDに記録されている音声データの波で、離散デジタル信号という)を、
- 幾つもの単純な紫色の波に分解して、
- 各紫色の波(周波数成分)ごとの強さを表現する青色のグラフを作る。
フーリエ変換の理論によれば、どのような複雑な波も、単純な波の組み合わせへと分解できるというのです。そのため、音声信号から周波数を取り出すということが可能になっています。理屈ではそうなんだろうとは分かるのですが、実際これを計算する方法を考えた人は天才だと思います。
ちなみに、「どのような複雑な波も、単純な波の組み合わせへと分解できる」ということを、動画で理解したい方は、次の3分46秒から5分12秒までをご覧ください。複雑な波が、単純な波の合成で作られていく様子がわかります。
「音の周波数」とは?
離散フーリエ変換を行うと、沢山の周波数(f)と振幅(A)の組が出てきます。"基本的には"これらの組の中で、最も振幅(A)の強い周波数が、その音の周波数になります。
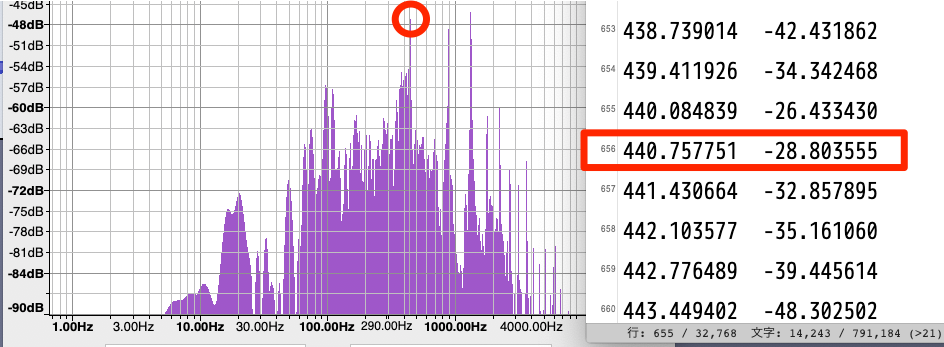
次の画像は、前回紹介したA4(440Hz)の音の解析例です。この例では、グラフでも、「周波数(f)と振幅(A)の組」でも、440Hzの周辺で最も振幅が強い 440.75...Hz がこの音の周波数(基音の周波数)ということになります。
ただ、グラフをよく見ると、右の1000〜4000Hzの間にもっと振幅の強い周波数(1322Hz)があります。第2回のコラムでも述べましたが、これは倍音成分のひとつです。実のところ周波数を解析すると、このように別の周波数成分が基音成分よりも強い場合がしばしば出てきます。
ですので、あくまでその音の平均律における周波数の周辺で、最も振幅の強い周波数を探す必要があります。
周波数の解析方法
以上の理屈を踏まえて、実際に音声編集ソフトのAudacityを使った周波数の解析をしてみます。
解析対象の音
解析対象には Upright Piano KW サウンドフォント のA2の音を用います。
次のファイルをダウンロードしてください: ↓ UprightPianoKW-A2vL.mp3
Audacityでのスペクトル解析
ダウンロードしたMP3ファイルをAudacityで開きます。
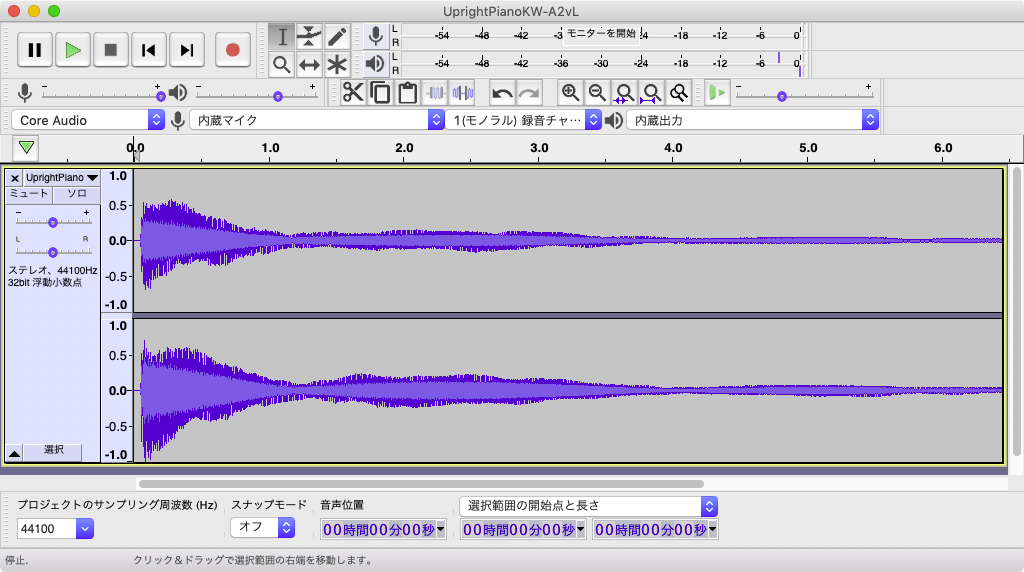
ここで、下部の「音声位置」の、音声位置表示の右の下三角マーク(▼)をクリックして、時間の表示単位を「時:分:秒+ミリ秒」に切り替えます。
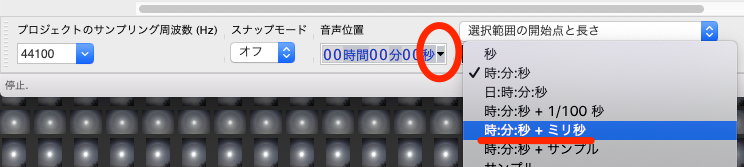
波形の先頭から、ある時間T秒をわずかに超えるだけの区間を選択します。このT秒は、左下に表示された「サンプリング周波数」をRとすると、65536÷R秒として求められます。
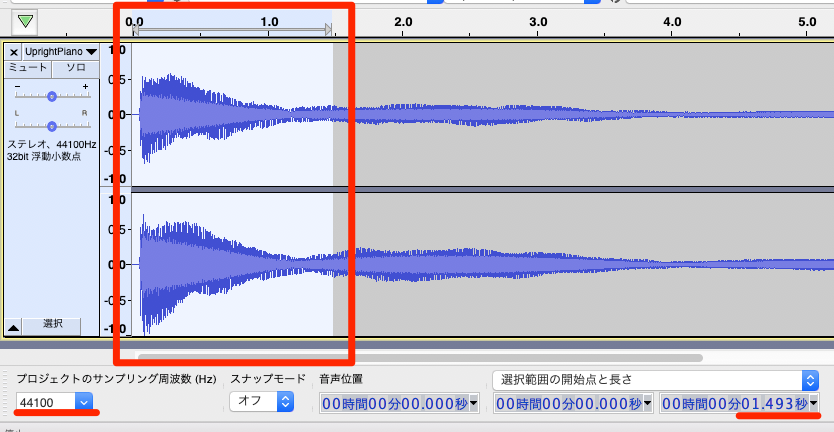
上の画像を例にとれば、サンプリング周波数は44100ですので、T=65536÷44100=1.486秒です。これをわずかに超えるだけの区間を選択するので、画像では1.493秒の区間を選択しています。(理由は付記として後述しています)
「解析」メニューから「スペクトル表示」を開きます。
次の「周波数解析」ダイアログが開きます。
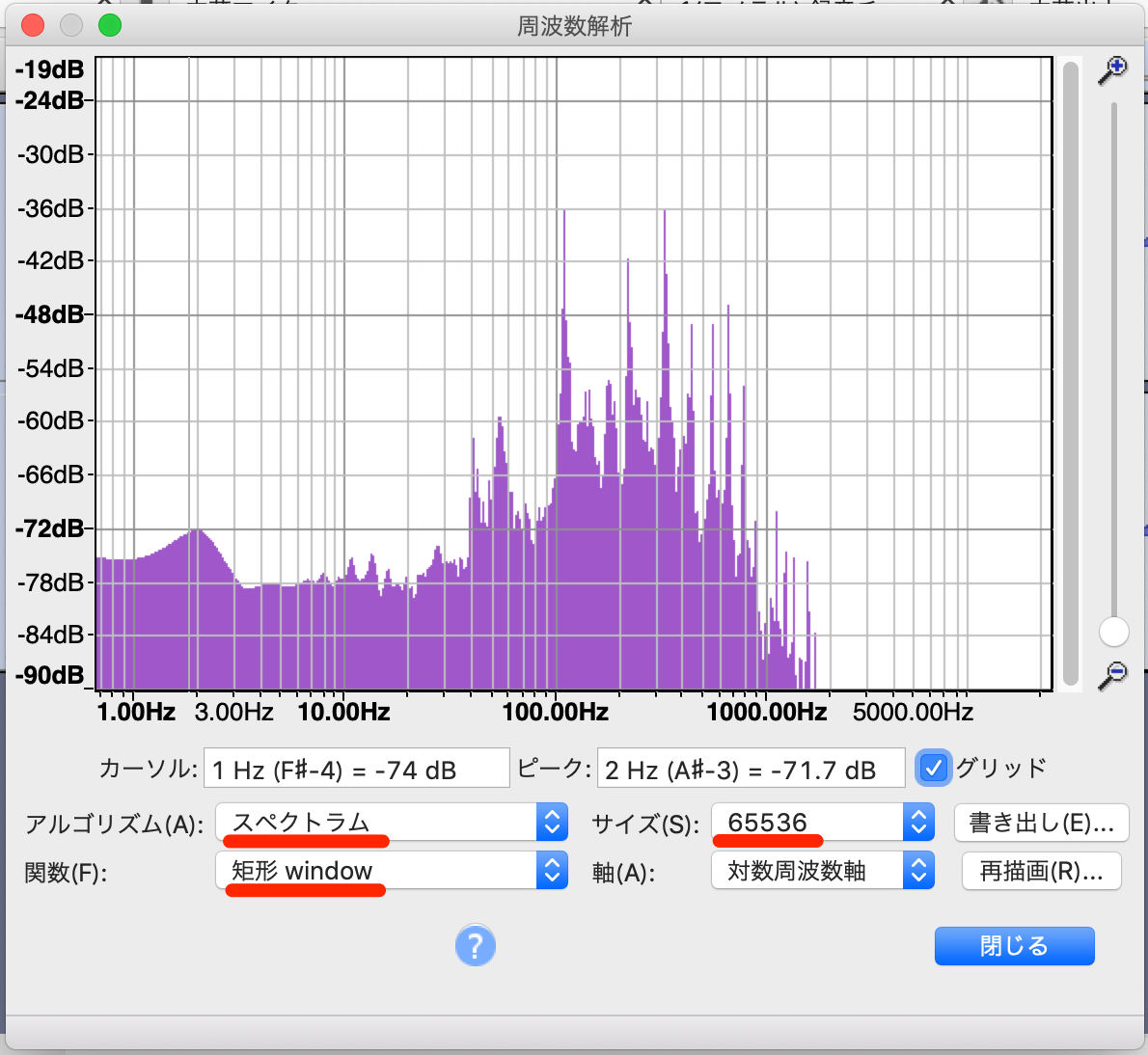
ここで、各所の設定を次の通りにします:
「アルゴリズム」
「スペクトラム」にします。これを選ぶと、離散フーリエ変換を行います。
「関数」
「矩形 window」にします。これは窓関数(その他参考1、参考2)を選ぶ箇所で、一般的には余分な(本来入っていない)周波数成分を落とすためHann window を用いることが勧められています。今回の様なケースは、解析結果のうち基音の強い周波数成分だけに注目するため、どちらでもほぼ結果は変わりません。
強いて言えば、入力信号に対し余分な操作をできるだけしない方が望ましいので、矩形窓(つまり窓関数を適用しないことと同じ)で良いと思います。もし解析がうまくいかない時は、Hann windowを試してみてください。
「サイズ」
最も大きく、先の区間選択でも用いた値「65536」を選びます。これは解析を行う信号の長さですが、実は離散フーリエ変換は、入力される信号の長さが長いほど、周波数の精度(分解能)が高くなるという性質があります。(参考)
既定では「4096」が選ばれていますが、これでは精度が10.6Hz刻み(計算式:音声データの"サンプリング周波数"÷サンプルサイズ = 44100 ÷ 4096 = 10.6 )になってしまい話になりません。「65536」を選ぶと、 44100 ÷ 65536 = 0.67 Hz刻みでの解析が可能になります。
最後に右の「書き出し」ボタンをクリックし、解析結果をファイルに書き出します。
◇ 付記 ◇
わざわざT秒(65536個の信号)だけを選択する理由ですが、Audacityのスペクトル表示は、選択した区間につき、サンプルサイズ分の区間ごとに離散フーリエ変換を行った結果を、平均して表示するためです。(参考)
今回の解析は、先頭の最も音の強い部分に対してだけ行えばよいものです。後半の無音部分も含んだ音声データ全体の平均は不要です。そのため、先頭から離散フーリエ変換をちょうど1区間だけ行った結果を表示するようにしています。
表計算ソフトでの調査
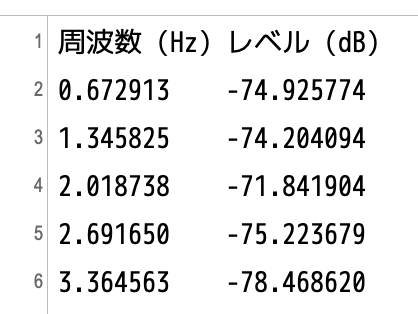
書き出したファイルには、次のように周波数とレベル(振幅のこと)の対がテキストになって入っています。
この書き出されたテキストを、Excelなどの表計算ソフトに貼り付け、「レベル」(振幅)で、降順に並べ替えます。
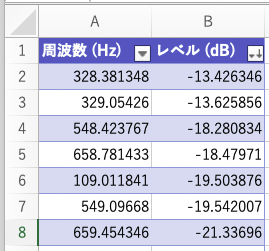
最も強い周波数は、328.38 Hzです。しかしこの音は A2 であり、平均律での音の高さとしては 110Hz 周辺の周波数になるはずですから、このような 110Hz から大きく外れた周波数は無視します。
すると、6行目に 109.01 Hz が見つかります。よって、この音の周波数は 109.01 ± 0.67Hz であると推定できます。
効率の良い解析プログラムについて
以上がAudacityを用いた手順です。前回書いた通り、音の数が多くなるとこの手順は大変なので、シャンティ・フーラでは上の解析を効率良く行うプログラムを作成しました。
本来、このプログラムを公開できれば調和純正律サウンドフォントを作りたい方の役に立つと思われるのですが、何分プログラムを公開できる状態まで整備して、サポートする余裕がありません。
このプログラムの中で一番面倒な部分は、音声ファイルを離散フーリエ解析し、基音周波数の取り出しを行う部分と思われます。その断片だけを公開しています。断片を活用して効率よく解析を行う方、もしくはツールを作成して公開する方が出てきてくださるようですとありがたく思います。
この回で、調和純正律による演奏を実現する方法の解説は終了します。次は最終回として、調和純正律の音律としての分析を試みたいと思います。
この記事は、シャンティ・フーラによる執筆記事です。音楽の分野に詳しい方におかれましては、もし間違いや説明上改善すべき点などがありましたら、ご指摘やご意見をいただければ幸甚です。ぜひ、こちらのコメント欄にフィードバックをお寄せください。




前回は、調和純正律サウンドフォントを作る過程を紹介しました。この中で、周波数の解析は意外と重要な過程です。
調和純正律の最大の特徴は、基準音高 A4 = 440Hz とこの音律から計算された各音の周波数が、経脈に作用するというところにあります。ですので、調和純正律サウンドフォントを作る元となる音の周波数を、出来る限り正しく調べることが重要なポイントになります。