調和純正律で遊ぼう ～第13回 調和純正律の分析（１）〜各音の間隔

第13回　調和純正律の分析（１）〜各音の間隔

はじめに 〜 調和純正律と純正律の違い

調和純正律は純正律を発展させた音律です。具体的には、第4回で述べたとおり、純正律イ長調の主音階7音に、竹下氏が独自に発見した周波数比による5つの半音を加えたものとなっています。

基にしている純正律と大きく異なる特徴として、各音の周波数が固定されているという点があります。つまり、純正律のように曲の調性にあわせて調律をすることはできません。（もしこれを行うと、各音の周波数が、経脈に作用する周波数からズレてしまいます。）

よって必然的に、調和純正律は、ひとつの調律で様々な調性の曲を演奏することを前提とした音律であるといえます。

すると、曲の調性によって、相性の良し悪しというものが出てきそうです。この最終回までの2回では、この点を判断するのに参考となる情報を提供したいと思っています。

古典音律2律

これまですでに、一般に知られる音律としては、十二平均律と純正律の2つを紹介してきました。今回はさらにもう2つの音律を紹介します。

どちらも、J.S.バッハが生きた時代である、バロック後期から用いられてきた有名な古典音律です。これらは、「ウェル・テンペラメント（「良く調整された音律」に近い意味の言葉）」といわれる音律で、それまで広く使われていた中全音律にかわって、多くの調をうまく演奏できるように作られたものです。


ヴェルクマイスターⅠ(Ⅲ)調律法

ヴェルクマイスターⅠ(Ⅲ)調律法(Wikipedia)は、J.S.バッハの友人であったヴェルクマイスターの発明した音律です。当時バッハが用いていた調律法はこれに近かったのではないかという説が、割と各所で見られます。

キルンベルガー第3法

キルンベルガー第3法(Wikipedia)は、J.S.バッハの弟子であったキルンベルガーが発明した音律です。師のバッハの教え「すべての長三度を純正より広くしなさい」に反して、1つだけ純正長三度を入れているのが面白いところです。

十二平均律との聴き比べ

上の２つの音律と十二平均律を、J.S.バッハの平均律クラヴィーア曲集第1巻より第17番 変イ長調(BWV862)・前奏曲で聴き比べてみましょう。（原曲はこちら）

①ヴェルクマイスターⅠ(Ⅲ)調律法

②キルンベルガー第3法

③十二平均律

①・②の古典音律を聴いたあと、③の十二平均律を聴くと、少々味わいが乏しく聴こえないでしょうか。音程をすっぱりと均等に割ってしまった十二平均律と比べて、古典音律には和音の響きが美しくなるような工夫が凝らされています。

①・②のどちらの音律も、この変イ長調の曲に用いた場合は、主音からの完全五度(A♭-E♭)は純正音程になり、良い響きが得られます。これらの音律の分析は、ストレングスビヨンドさんのサイトが分かりやすいです。

各音の間隔の比較

それでは、各音律を分析的に比較してみましょう。今回は、各音の間隔です。


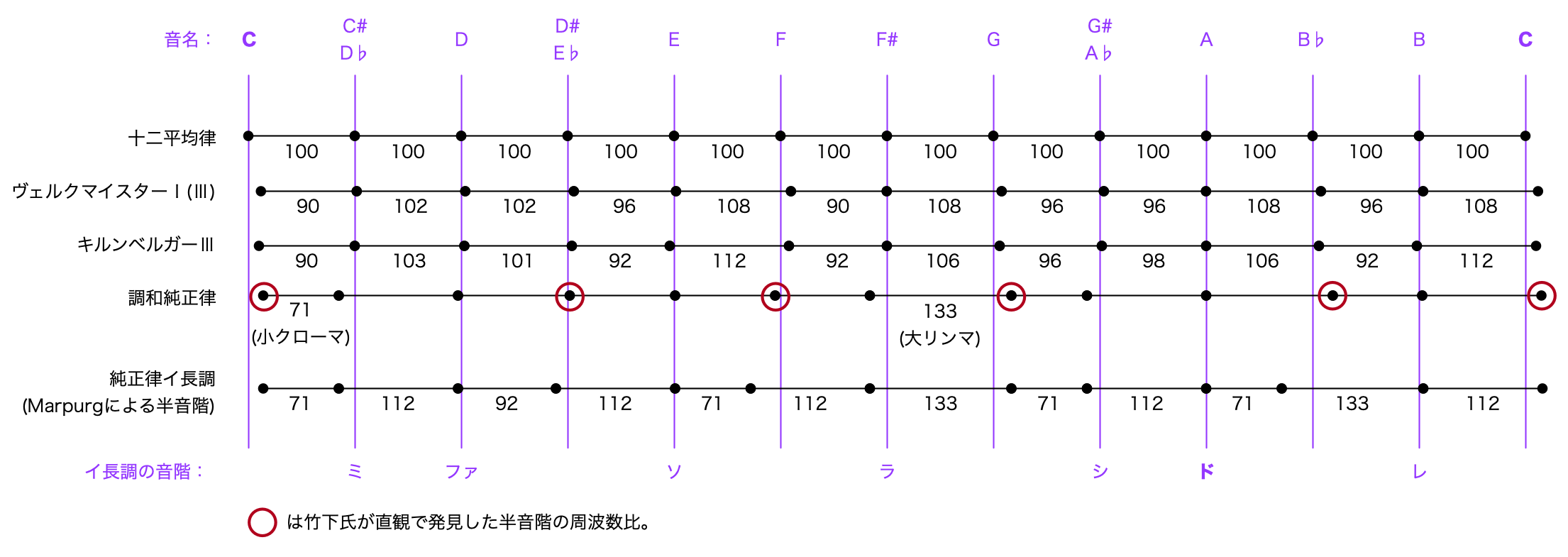
Aの音を基準にして、音律ごとに各音の間隔を比較しました。一番上に音名、一番下にイ長調の音階名を付しています。

こうして見ますと、ヴェルクマイスター／キルンベルガー音律は、音の間隔がバランスよく、十二平均律に近くなっています。この点でも、様々な調での演奏に適しているわけです。

いっぽう調和純正律は、純正律の調律法群の一部に見られる小クローマ・大リンマと呼ばれる、極端な半音の間隔があらわれます。このあたり、バランスが崩れやすく、調性を選ぶところかもしれません。

偶然の一致と竹下氏の周波数比の調べ方

さらに、面白い発見があります。純正律の半音の取り方の中に、マールプルグ(Marpurg,1718-1795)による調律法があるのですが、上の図ではこれを調和純正律の下に記載しました。このマールプルグの半音の取り方は、竹下氏が直観で導いた半音の周波数比群と一部共通点があります。

とりわけ、CとGの周波数比が偶然にも一致し、このため小クローマ(71セント)1つと大リンマ(133セント)1つが、まったく同じ箇所に登場することは驚きです。マールプルグは純正長3度を用いてこの2音の周波数比を求めたと思われますが、竹下氏は同じ数字を直観で選び取っています。

竹下氏の周波数比の調べ方が分かる部分を、東洋医学セミナーから抜粋します：



東洋医学セミナーは、理屈を超えた感覚で正解を選び取る技術と感受性を磨く講座です！　この世界に興味を持たれた方は、ぜひ受講してみてください。

今回は、上の意外な発見があり長くなったので、最終稿を2回分の記事に分けることにしました。次の最終回は、五度圏を用いて調和純正律を分析します。